Logboek 2010/1 (Kreta>Fethiye)

Een brigade zwerfkatten houdt de wacht bij de achterdeur van het supermarktje naast de kade

Woensdag 02-06-2010

We aten gisteravond op een terras onder de bomen in een straatje van het dorp. De atmosfeer, de huizen en de grote schaduwrijke bomen, het doet op een of andere manier een beetje Turks aan. Ook hier dateert het gebouwtje van de havenpolitie net als in Kárpathos uit de Ottomaanse tijd. Er zijn hier beduidend meer toeristen dan op Chalki, dat we overigens pittoresker vonden. Direct naast de kade is een kleine supermarkt. Bij de achterdeur houdt een contingent schriele zwerfkatten de wacht (foto hierboven). Ze zien er uitgemergeld, ziek en brutaal uit.´s Avonds schuimen ze de eetgelegenheden af, op zoek naar wat van de tafels valt of hen toegeworpen wordt. Voor het slapen sluiten we uit voorzorg de luiken en de raampjes; ze zijn brutaal genoeg om aan boord te sluipen en onze Lord Byron de stuipen op het lijf te jagen.

Vanochtend is het heiig en in het zuiden bewolkt. Er zou een koufront met wat regen overkomen. De huurboten en het flottielje vertrekken, voor tienen is iedereen weg. Ze hebben een strak schema en moeten op tijd terug zijn om de boten weer in te leveren. Wij blijven met een andere zeilzwerverboot als enigen een dagje liggen en prijzen ons daarmee gelukkig.

Behalve boodschappen doen bestaat de dag vooral uit lezen. Ik begraaf me weer eens diep in fysica en kosmologie met beide boeken van Brian Greene bij de hand, "The Elegant Universe" (1999, Vintage) en "The Fabric of the Cosmos" (2004, Penguin) Goede boeken, ik vind dat die man elke vijf jaar zo´n boek moet schrijven. Het gaat me dit keer vooral om de implicaties van zwarte gaten in verband met de Tweede Wet van de Thermodynamica. De wet die zegt dat alles in het universum (en het universum zelf) zich beweegt in de richting van toenemende wanorde (entropie) Deze wet maakt deel uit van het Werkprogramma van vijf raadselachtige zaken dat ik me een paar jaar geleden voornam.

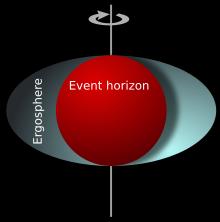
 Zwarte gaten in het heelal bezitten de maximaal mogelijke entropie. Ze beslaan dus een gebied dat niet nog méér wanorde kan bevatten. Het merkwaardige is dat dat feit niets te maken heeft met het volume van een zwart gat, zoals je zou denken, maar met de grootte van zijn oppervlak. Dus niet wat erin kan, maar wat erop kan. Wat is de oppervlakte van een zwart gat? Zoals je waarschijnlijk wel weet is een zwart gat een structuur - klein of groot - waarin zoveel materie uiterst dicht opeen geperst zit dat het een enorme zwaartekracht uitoefent. Zoveel dat er niets uit het gat kan ontsnappen, zelfs licht niet, terwijl een lichtdeeltje helemaal niet eens massa heeft. Een zwart gat is dus letterlijk zwart. Door zijn grote zwaartekracht trekt het alle materie in de buurt naar zich toe en slokt die op en voegt het bij de materie in zijn kern. Toch wordt zijn entropie daardoor niet groter, die is immers al maximaal. Het volume en het oppervlak moeten dus groter worden. Rekenkundig is het zo dat het volume drie keer sneller groeit en het oppervlak slechts twee keer sneller. Wat is - nogmaals - eigenlijk het oppervlak van een zwart gat? Ieder zwart gat heeft een event horizon vanaf waar materie niet meer aan de aanzuigende kracht kan ontsnappen en reddeloos opgeslorpt wordt. Zie het plaatje hiernaast. De event horizon is als het ware een bol waarop alle points of no return liggen. Stel nu dat je op het oppervlak van die bol een soort schaakbordpatroon van zoveel mogelijk vierkantjes zou maken. In de moderne fysica kan niets kleiner zijn dan de

zogenaamde Planck-lengte, en het kleinst mogelijk vierkant zou je een Planck-vierkant kunnen noemen van ongeveer 10^-66 cm²  In de jaren ´70 van de vorige eeuw ontdekten Jacob Bekenstein en Stephen Hawking dat deze minimale fundamentele ruimte-eenheid slechts één eenheid van entropie kan bevatten.

Okay, waar gaat het nu om? De quantumfysica heeft een eind gemaakt aan het determinisme, dat als je alle posities en snelheden van alle deeltjes in het heelal op zeker ogenblik zou weten, je de toekomst van het heelal zou kunnen berekenen. In de quantum-fysica kom je niet verder dan het berekenen van waarschijnlijkheden. Dat wordt wel een soort quantum-determinisme genoemd. Geen determinisme van zekerheden maar dan toch tenminste van waarschijnlijkheden. Dezelfde Hawking berekende in 1976 dat zelfs dat niet mogelijk is. Dat komt door de vraatzucht van de zwarte gaten. Van materie die erin valt gaat alle informatie verloren, zo was het idee, en dus ontbreekt die in de becijfering van een waarschijnlijke toekomst. Over dit punt bestaat echter geen overeenstemming. Sommige fysici beweren dat die informatie weer beschikbaar komt als het zwarte gat zich in de tijd oplost. Ze hebben er zelfs een weddenschap met Hawking over afgesproken die ruim dertig jaar later nog door niemand gewonnen is.

In de kern van het zwarte gat zit materie zó onvoorstelbaar dicht opeen geperst, dat sommigen denken dat de materie er geen toekomst heeft omdat de tijd er stil zou staan. Als men Einsteins vergelijkingen toepast op die kern, ontstaat een mogelijkheid dat het een poort vormt tot een ander universum. Waar de tijd in ons universum tot stilstand komt, zou de tijd in het andere universum juist beginnen. Duizelingwekkend allemaal, je zou zolang willen leven tot het duidelijk wordt maar daar is weinig kans op. Helemaal géén kans, eigenlijk, mijn voornoemde werkprogramma is een onmogelijke opdracht. Hoe treurig. Maar niet nieuw en geen reden om ermee te stoppen.

Eind van de middag. Andere schepen, voor de helft huurboten en de andere helft zee-nomades als wij, liggen aan de kade. Ik help een huurboot met Duitsers met een verlengsnoer. Regen is er niet gekomen, de zon schijnt weer onbarmhartig en het is benauwend warm. Overigens kan je ons zien. Het reisbureautje Tilos Travel heeft een webcam die op de kade gericht staat. We gaan niet staan zwaaien. Terug naar boven